Les réseaux de Pétri

INTRODUCTION

Ils furent inventés en 1964 par Carl Adam Pétri.

Il est important de noter que les réseaux de Pétri constituent un outil très puissant. Cependant, il n'a pas pénétré le milieu industriel faute de normes et d'une utilisation souvent trop tournée vers la recherche que vers l'industrie. C'est sa forme voisine, le Graphcet qui s'est répandu dans le milieu industriel. De nos jours, l'industrie requiert des outils de modélisation de plus en plus puissants, et le Graphcet montre parfois ses limites.

Peut-être les réseaux de Pétri remplaceront-ils un jour le Graphcet?

Le Graphcet est une forme voisine des réseaux de Pétri. Nous présenterons tout d'abord ces deux outils de modélisation, puis nous établiront une comparaison.

I)LE GRAPHCET

cf cour

II) PRESENTATION DES RESEAUX DE PETRI

a) Définitions essentielles

Une place

Une pace décrit les états du système modélisé. C'est un rond.

C'est l'équivalent du carré dans le Graphcet

Une transition

Elle représente les changements d'état. C'est l'équivalent du __ au Graphcet

Un arc orienté

Ce sont les arcs orientés qui relient les places aux transitions. A chaque arc est associé un nombre, appelé "poids de l'arc"

Un jeton ou une marque

Ils sont placés dans les places.

Exemple récapitulatif : fig1

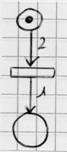
fig 2 :Le nombre de jeton est inférieur au poids de l’arc. Donc la transition n’est pas franchie

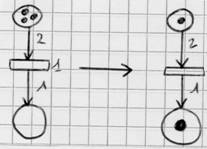
fig 3 :Le nombre de jeton est supérieur au poids de l’arc, la transition est donc franchie

b) Propriétés essentielles

Arc orienté

En général, le poids de l'arc=1, c'est un réseau de Pétri ordinaire.

Quand le poids de l'arc différent de 1, on parle de réseau de Pétri généralisé. On met dans la place

Sensibilisation d'une transition: quand le nombre de jetons dans la place d'entrée est supérieur au poids de l'arc

Franchissement d'une transition
On prélève dans la place d'entrée un nombre de jetons égal au poids de l'arc issu de la transition.

Quand la transition est sensibilisée et que la réceptivité associée à la transition est vrai.

c) Parallélisme et synchronisation

Le parallélisme et la synchronisation sont les deux grandes caractéristiques des systèmes séquentiels.

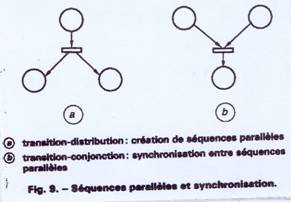
Synchronisation de séquences parallèles.

Quelques exemples: Il faut que lest transitions de droite et de gauche soient sensibilisées. :

3 jetons au minimum à gauche

2 jetons au minimum à droite

c=1

Étape d’attente

Synchronise les 3 branches

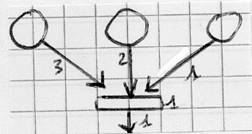
fi4 :Le 1 sur la transition signifie que la condition associée à cette transition est toujours vraie.

Création de séquentielles parallèles

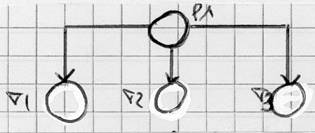
fig 5

Bilan (fig 6):

d) l'extension temporisée

On intègre au réseau de Pétri la variable temps. Cette référence de temps se superpose au modèle autonome qui devient de facto non autonome.

Le tout est appelé "réseau de Pétri temporisée".

Le P-temporisé

Ce sont les places qui sont temporisées

Le T-temporisé

Ce sont les transitions qui sont temporisées. Remarque: On montre que 1 est équivalent à 2

Le Pétri interprété

Lorsqu’il existe des réceptivités sur les transitions

e) Quelques types de réseaux de Pétri

Réseau de Pétri borné

Quand le nombre de jeton dans les places ne dépasse pas un nombre k

Réseau de Pétri pseudo vivant

Si pour à tout instant il existe une transition sensibilisée. Dans la pratique cela se traduit par une absence de blocage.

Réseau de Pétri vivant

Si toutes les transitions peuvent être franchies.

Réseaux de Pétri propre (réinitialiser)

Il existe un cycle tel qu’à un moment donné, lors du fonctionnement, la configuration du réseau est la même qu'à l'état initial.

f) L'interprétation, la traduction mathématique.

Les réseaux de Pétri peuvent être modélisés par des matrices.

g) Conflits

Conflit structurel

C'est quand une transition possède une entrée commune

Conflit effectif

C'est lorsqu’un marquage sensibilise les deux transitions

En fait, rien dans le réseau ne permet de prévoir laquelle des transitions sera franchie.

Exemple :

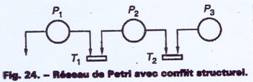
Fig 7

II Comparaison du réseau de Pétri et du Graphcet sur un exemple

a) L’exemple : Partage de ressource

Soient deux chariots C1 et C2 qui se déplacent indépendamment l’un de l’autre sur 2 voies distinctes.

Le bouton M1 actionne C1 s’il est en A1

Le bouton M2 actionne C2 s’il est en A2

Le cycle A1-B1-A1 (resp A2-B2-C2) avec chargement A1(resp A2) et déchargement en B1 (resp B2)

Le déchargement de C1 est prioritaire sur C2.

Soit :

CHG1 : Chargement du chariot C1

CHG2 : Chargement du chariot C2

DCHG : Déchargement

FINCHG1 : Fin de chargement du chariot C1

FINCHG2 : Fin du chargement du chariot C2

FD : Fin de déchargement

Le réseau de Pétri :

1, B1 : Priorité

Synchronisation

Le Graphcet : C1 C2

b) La Comparaison :

Outre la symbolique, la principale différence est la gestion de la synchronisation :

Graphcet : Utilisation de P13 et forme graphique

Pétri : Meilleure visualisation de la synchronisation :

è liaison plus claire

è fort intérêt pour des commandes complexes avec beaucoup de synchronisation

Cf Graphcet d’un contrôle précédent (assez compliqué)

Par contre, la priorité de C1 sur C2 est gérée de la même façon avec une réceptivité alliée à une transition.

On peut aussi voir qu’avant cette priorité tous deux possèdent une étape d’attente.

On remarque aussi que (Hormis P13), les deux graphes (Graphcet et Pétri) possèdent le même nombre d’étapes (12)

CONCLUSION

Malgré leurs spécificités propres, le Graphcet et le Pétri sont très proches dans le traitement des commandes séquentielles.

Néanmoins, au travers de cet exemple, nous avons pu constater que Pétri aborde le problème avec une conception plus schématique et graphique ; ce qui lui octroie un avantage dans la compréhension de la commande d’autant plus quand cette dernière est complexe.

Or, de nos jours les commandes séquentielles ont tendance à se complexifier, ce qui encourage l’utilisation de Pétri. De plus, il existe une adaptation de Pétri : les Pétri coloriés qui permettent d’aborder des problèmes plus complexes avec une conception encore plus visuelle.